满二叉树:如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,那么这就是满二叉树。如图所示:
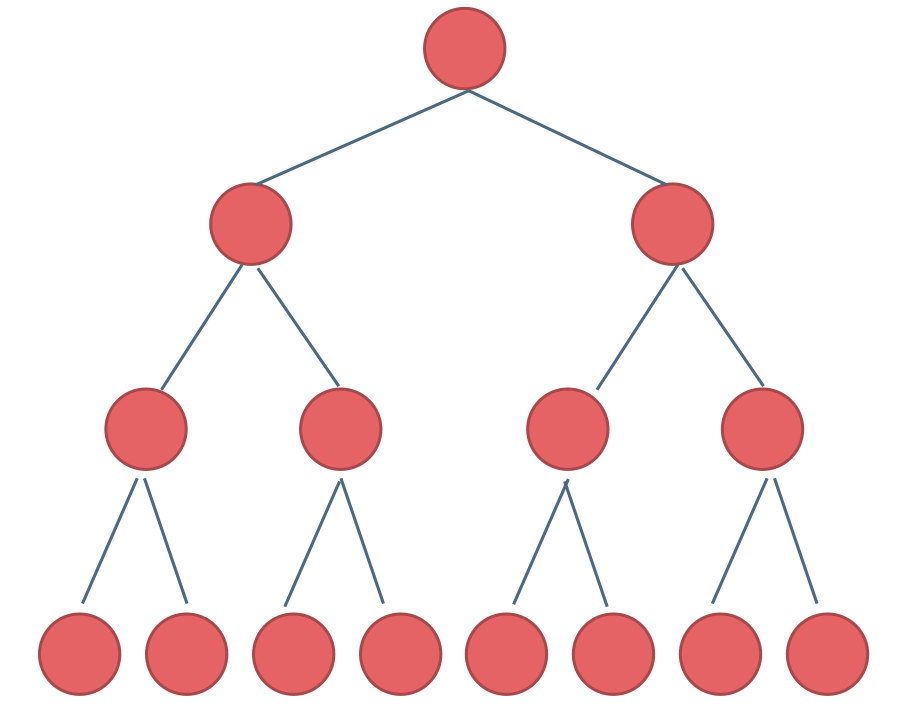
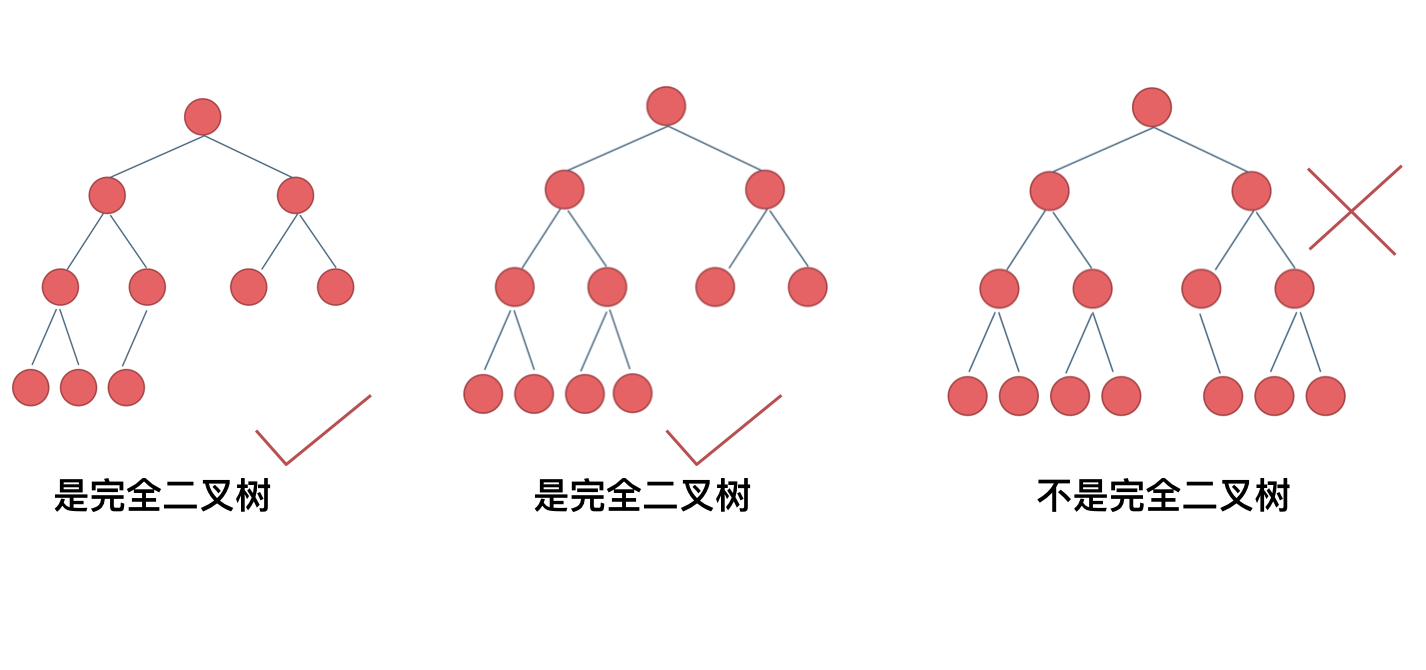
完全二叉树:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在最左边的若干位置。如图所示:
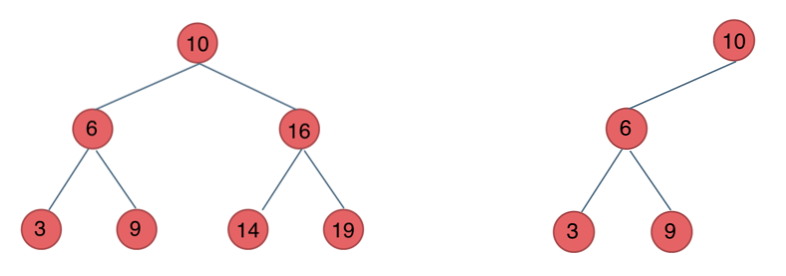
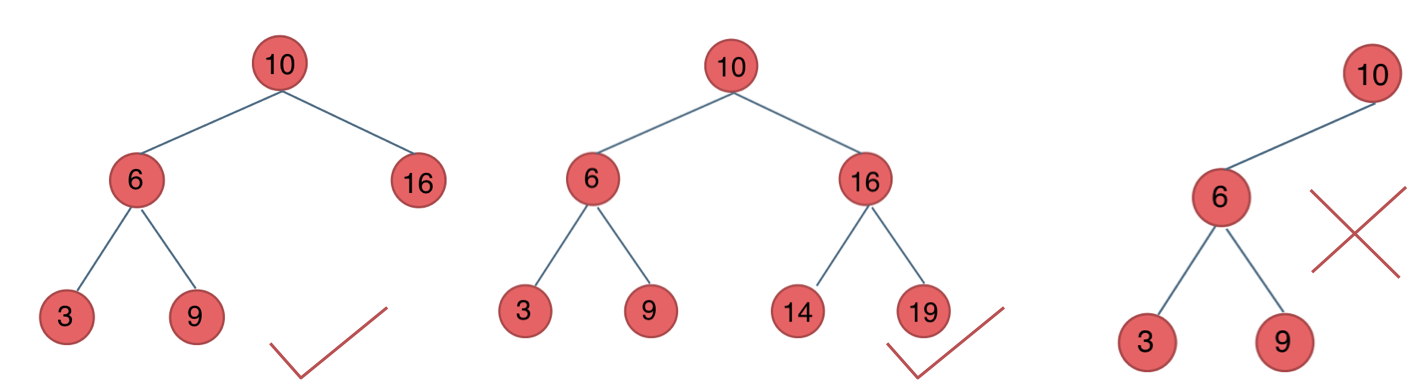
二叉搜索树:前面介绍的树都没有数值,而二叉搜索树是有数值的,且是有序树,又名二叉排序树。满足如下的条件:
1)若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2)若又子树不空,则右子树上所有节点的值均大于它的根节点的值;
3)它的左、右子树也分别为二叉搜索树。
平衡二叉搜索树:又叫AVL树(Adelson-Velsky and Landis),具有以下性质:它是一颗空树或他的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是平衡二叉搜索树。
二叉树的存储方式
二叉树可以链式存储,也可以顺序存储。
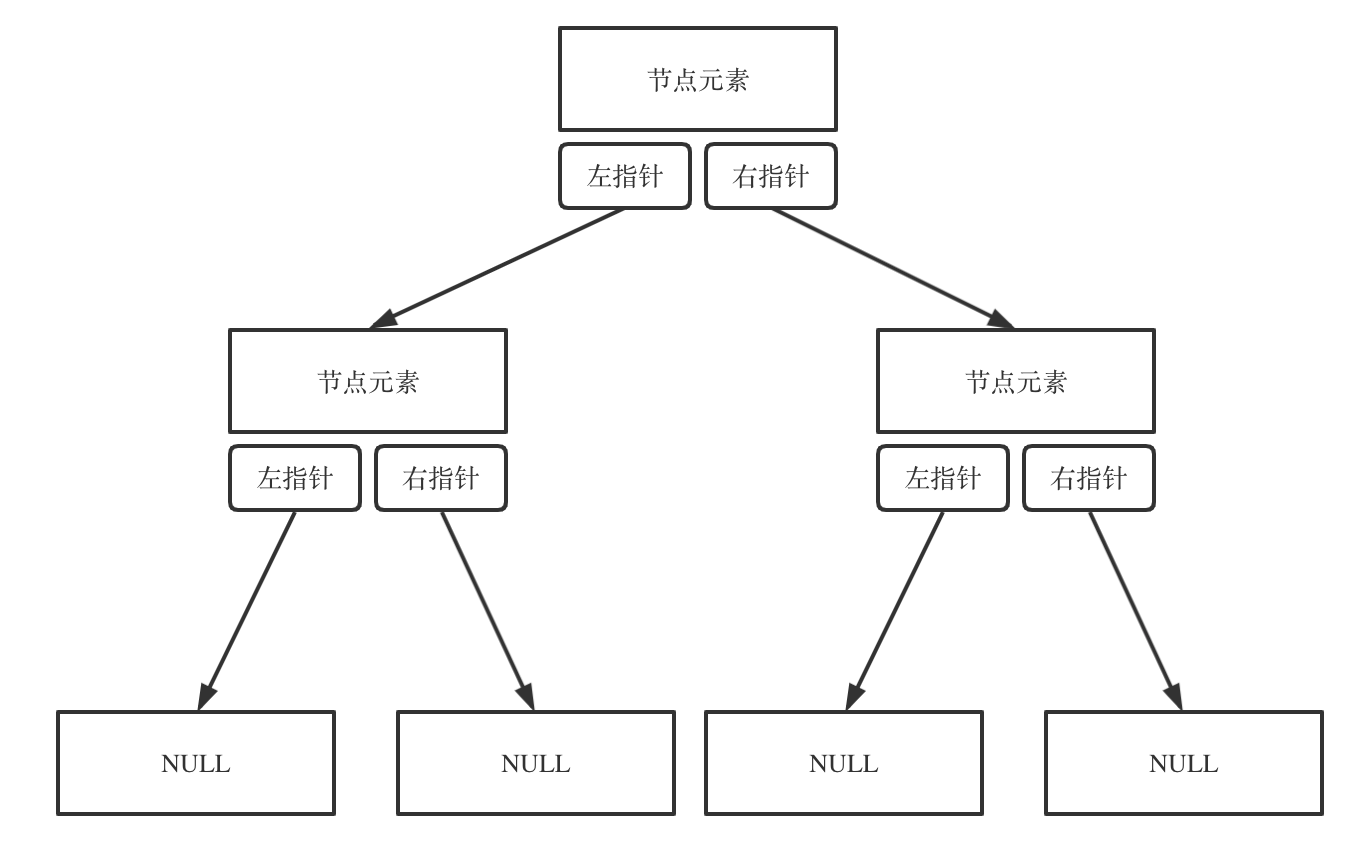
链式存储方式是用指针,和链表结构类似,顺序存储方式是用数组。
链式存储如图:
顺序存储如图:
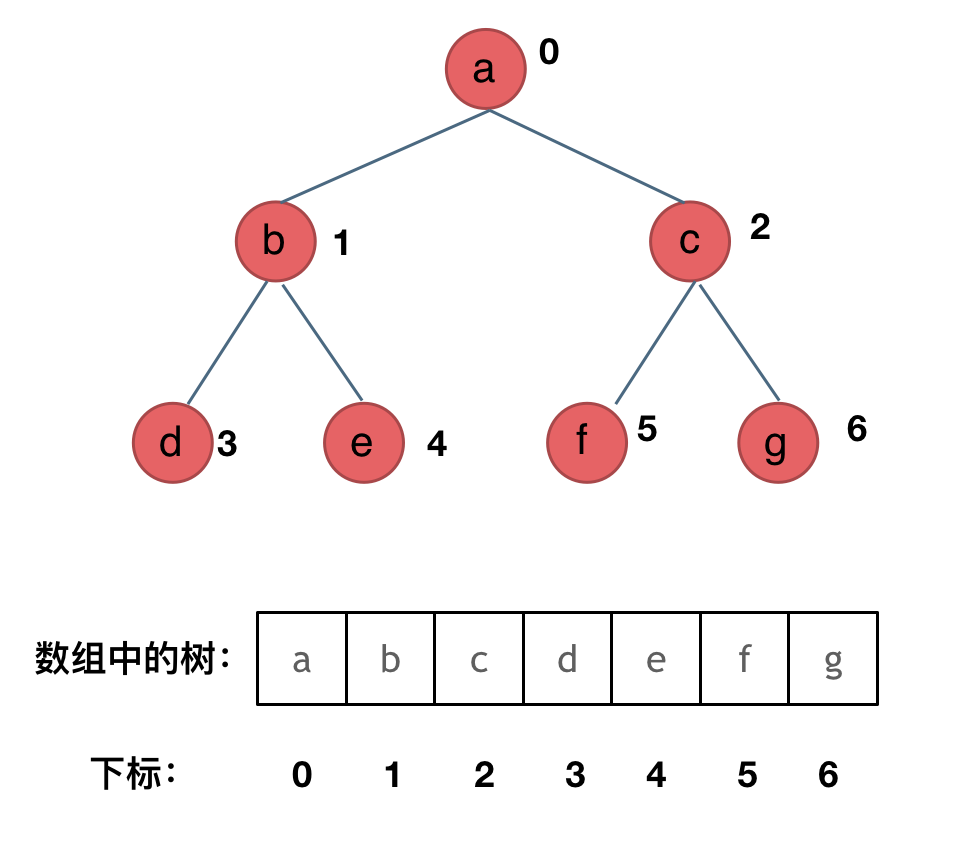
用数组存储二叉树,应该如何遍历呢?如果父节点的数组下标是i,那么它的左孩子就是i2+1,右孩子就是i2+2。
二叉树的遍历方式
二叉树有两种遍历方式:
1.深度优先,先往深走,遇到叶子节点再往回走;
2.广度优先,一层一层的去遍历。
其中,深度优先有三种顺序:
1)前序遍历(递归法,迭代法);
2)中序遍历(递归法,迭代法);
3)后续遍历(递归法,迭代法)。
广度优先仅有一种方式,层次遍历(迭代法)。
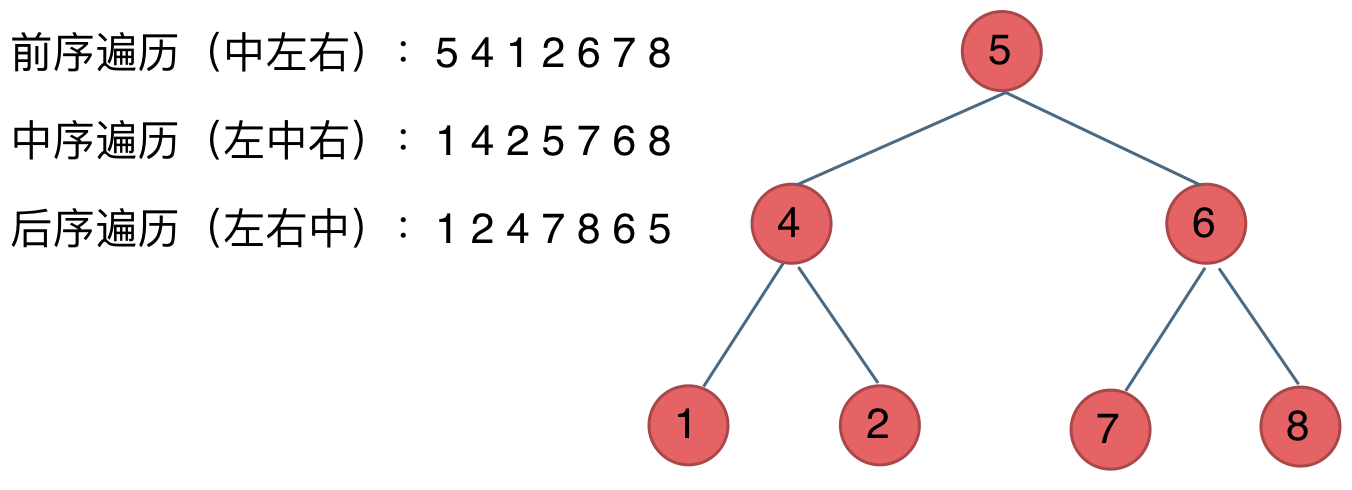
深度优先三个遍历顺序容易搞混,一个有效的技巧是,前中后序指的是中间节点的位置:
前序遍历:中左右
中序遍历:左中右
后续遍历:左右中
例如图:
代码实现:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode() {
}
public TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}